Una de las aplicaciones importantes de la termografía es la determinación de la transferencia de calor por radiación, a partir de la estimación de la emisividad media y de las temperaturas superficiales de los elementos que están realizando el intercambio de calor.
Como todos los cuerpos emiten radiación por encima de los cero grados absolutos de temperatura, sin importar el medio (incluso en el vacío), y todos presentan diferentes propiedades radiativas, en cualquier circunstancia, el análisis de transferencia de calor por radiación se vuelve muy complejo porque la transferencia es el resultado de la interacción entre las emisiones particulares y las reflexiones, transmisiones y absorciones de los cuerpos involucrados en el análisis. Aparte de considerar que los mecanismos de transferencia de calor (conducción, convección y radiación) no se presentan en forma independiente sino que son simultáneos.
Para el análisis de radiación es necesario involucrar el término de factor de visión o factor de forma que entre superficies difusas se define como Fij, que es la fracción de la radiación que sale de la superficie i y choca contra la superficie j, independiente de la temperatura y de las propiedades de la superficie.
Relaciones fundamentales del factor de visión
Las relaciones fundamentales sirven para determinar los factores de visión entre diferentes superficies desde algunos valores conocidos. Tales relaciones son:
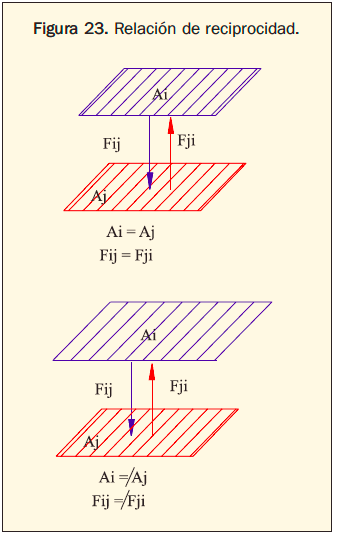
1. Reciprocidad. Los factores de visión Fij y Fji no son iguales entre sí, a menos que las áreas de las dos superficies lo sean (figura 23).
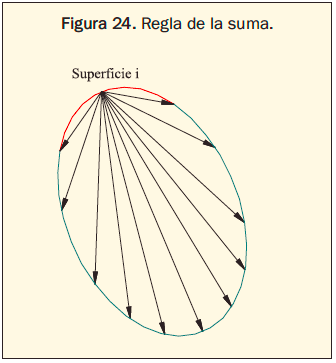
2. De la suma. La suma de los factores de visión desde la superficie i de un recinto cerrado hacia todas las superficies del propio recinto hasta, incluso hacia sí misma es igual a 1 (figura 24).
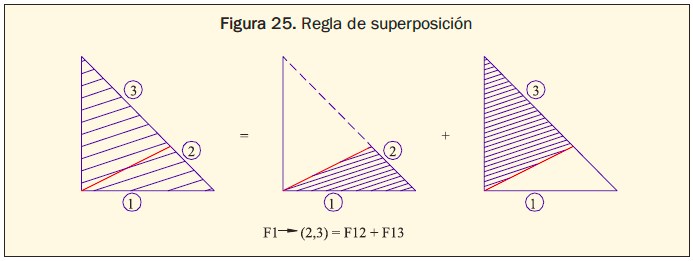
3. Superposición. El factor de visión desde una superficie i hacia una superficie j es igual a la suma de los factores de visión desde la superficie i hacia las partes de la superficie j (figura 25).
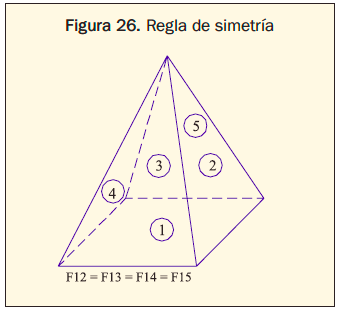
4. Simetría. Dos o más superficies que poseen simetría con respecto a una tercera tendrán factores de visión idénticos desde esa superficie (figura 26).
Métodos adicionales: Un método útil para determinar los factores de forma es el método de las cuerdas cruzadas desarrollado por H.C Hotel en la década de 19501 y representado en la figura 27.
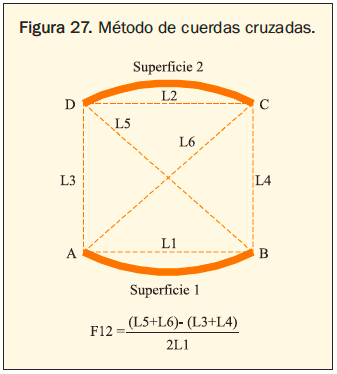
El método es aplicable cuando se considera conveniente trabajar en dos dimensiones puesto que cualquier interacción por radiación a través de los extremos es prácticamente despreciable o incluso cuando las dos superficies consideradas comparten una arista común, como un triángulo.
Otros métodos son los gráficos que para la aplicación particular representan los factores de forma en función de las geometrías de las superficies y espacios involucrados.
Solución de problemas:2 Las fracciones de energía emitidas entre las superficies se pueden determinar a partir de los factores de forma, las propiedades radiativas y temperaturas de cada superficie involucrada. Existen dos métodos complementarios para la solución de problemas sobre radiación así:
Método 1. Para superficies con velocidades específicas de la transferencia de calor.
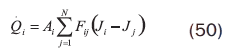
Método 2. Para superficies con temperatura específica Ti.
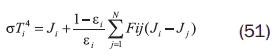
Donde J corresponde a la energía total de radiación que sale de una superficie por unidad de tiempo y por unidad de área, sin importar su origen, es decir energía emitida y reflejada, denominada radiosidad. De manera que para una superficie gris y opaca se puede expresar así:
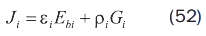
Donde:
εiEbi = Radiación emitida por la superficie i.
ρiGi = Radiación reflejada por la superficie i.
Cuando una superficie es aislada térmicamente a la radiación, pierde tanta energía de radiación como la que gana3 y en tal caso Qi = 0, en la ecuación 50. Si se trabaja con un cuerpo negro (ε = 1), entonces la radiosidad será igual a la energía emitida por un cuerpo negro (σT4), porque el segundo término de la ecuación 51 desaparecerá.
A partir de las ecuaciones 50 y 51 se obtienen N ecuaciones para determinar N radiosidades al interior de un recinto con N superficies. Conocidas las radiosidades, se pueden determinar las velocidades de transferencia de calor con la ecuación 50, y las temperaturas desconocidas con la ecuación 51. Si se presentan superficies aisladas (reirradiantes) las temperaturas se calculan a partir de la relación σTi 4 = Ji. Si el valor de Qi es negativo, significará que la superficie está recibiendo la radiación.
Ejemplo: Considere un horno cilíndrico vertical con condiciones de operación estacionarias, de radio 1m y altura 2m, como se muestra en la figura 28.
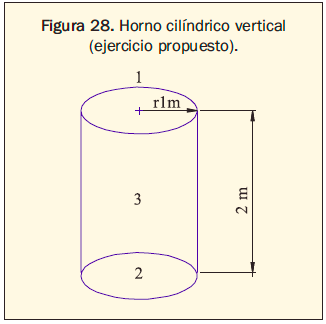
Las superficies superior 1, inferior 2 y cuerpo 3, tienen emisividades de 0.7, 0.3 y 0.5; y temperaturas de 950K, 560K y 440K respectivamente. Determinar la transferencia neta de calor por radiación en cada superficie.
Solución: En la Tabla 8 se encuentra descrito el procedimiento para dar solución al ejercicio.
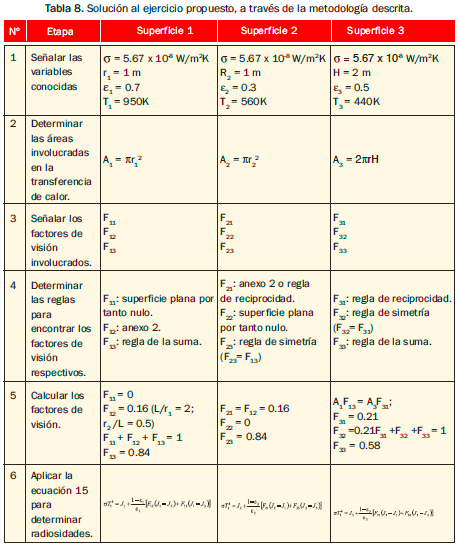
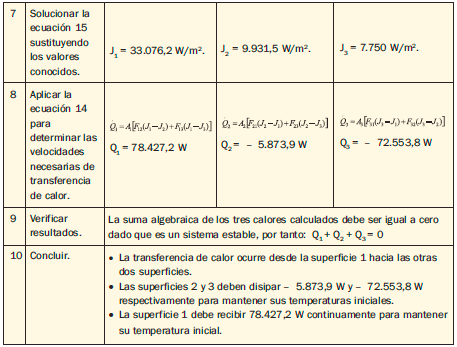
Un método alternativo para determinar la transferencia de calor por radiación consiste en el análisis por circuitos térmicos al igual que se hacía para solucionar problemas de conducción y convección. En este capítulo no se realiza su explicación porque no hace parte del propósito principal del mismo, sin embargo en la sección 5.2 del capítulo IV 4se aplica directamente para determinar la transferencia de calor por radiación entre una caldera y el recinto que la contiene.
- Cengel Yunus A. Transferencia de Calor. Segunda Edición. Mc Graw Hill. México, 2004, cap 12. ↩︎
- INCROPERA y DeWITT. Fundamentos de Transferencia de Calor. México. Prentice Hall, 1999, cap 13 ↩︎
- Concepto general de una superficie reirradiante. ↩︎
- Jorge René Silva Larrotta, Introducción A La Termografía Industrial. Universidad Libre – Bogotá. 2006. ISBN 978-958-97987-0-6 ↩︎
*Fuente: Jorge René Silva Larrotta, Introducción A La Termografía Industrial. Universidad Libre – Bogotá. 2006. ISBN 978-958-97987-0-6
