Es un mecanismo relacionado directamente con la interacción molecular entre partículas de mayor energía con unas de menor energía, ocasionada por la diferencia de temperaturas entre dos límites imaginarios o físicos de un sistema.
Naturalmente las partículas sometidas a una temperatura mayor presentarán un mayor movimiento que se transmitirá a las ubicadas en las zonas de menor temperatura, de manera que el flujo de calor ocurrirá en la dirección donde la temperatura disminuye.
El modelo matemático que cuantifica la transferencia de calor por conducción es la ley de Fourier, que para una placa plana unidimensional se presenta en la figura 17.
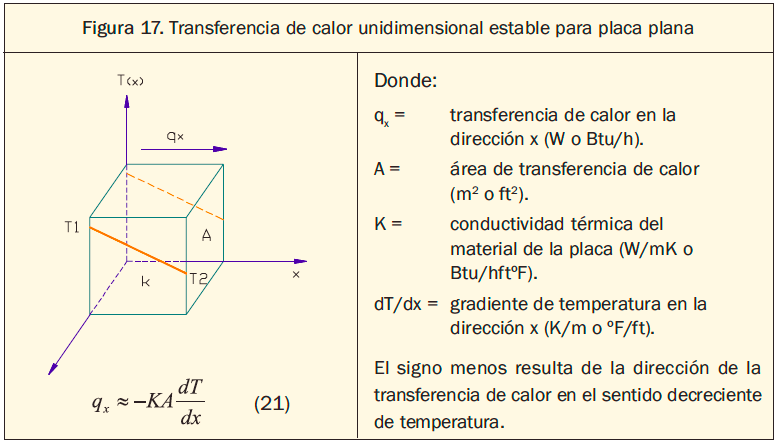
La conductividad es una propiedad particular de cada material y en términos simples se asocia con la facilidad de transmitir calor por conducción. En la mayoría de los casos se relaciona con la conductividad eléctrica, de manera que por lo general los materiales altamente conductores de electricidad son altamente conductores del calor. En los sólidos su valor es muy superior que en los fluidos debido principalmente al espacio intramolecular existente que los hace menos efectivos.
A pesar de presentar una fuerte dependencia con la temperatura, en evaluaciones básicas de ingeniería se trabaja con un valor medio entre las temperaturas de operación del proceso.
A partir del análisis de la conducción no sólo se determina la transferencia de calor en un sólido sino también su distribución de temperaturas, constituyéndose en un instrumento útil en la valoración de propiedades térmicas, esfuerzos, expansiones, etc. Para determinar tal distribución se realiza un balance de energía a un volumen de control diferencial considerando el flujo de energía por difusión en las tres direcciones, su posible generación interna de energía por unidad de volumen (Eg) a causa de un proceso particular y su energía almacenada (E alm), como se muestra en la figura 18.
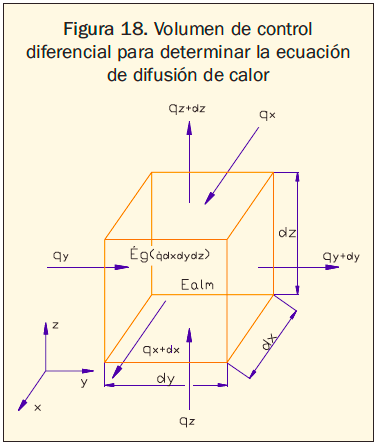
El resultado final es la ecuación de difusión de calor y establece que para un elemento diferencial dentro del medio, la suma de la rapidez de transferencia de calor por conducción y de la energía generada es igual al cambio de energía térmica almacenada:
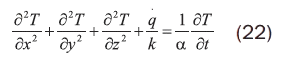
Siendo q el calor generado por el elemento diferencial, k la conductividad térmica, α la difusividad térmica (k/ρCp), ρ la densidad y Cp el calor específico del sólido.
Cuando el sistema es estable la ecuación se simplifica así:
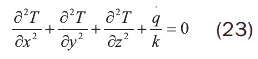
Y si no hay generación de calor:
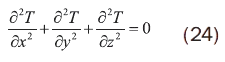
Si la transferencia de calor es de carácter unidimensional, estable y sin generación de calor:
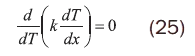
Ecuación que al resolverse para la geometría sencilla de placa plana, considerando la conductividad térmica constante y las condiciones de borde adecuadas, entrega la distribución lineal de temperaturas como se ve en la figura 19:

Al realizar la evaluación de la distribución, fácilmente se puede determinar la transferencia de calor con la ley de Fourier:
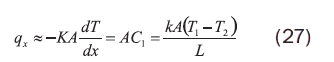
Resultado que se puede asociar con la ley de Ohm de circuitos eléctricos, porque el flujo de corriente es proporcional a un diferencial de voltaje e inversamente proporcional a una resistencia eléctrica, en tanto que la transferencia de calor es proporcional a una diferencia de temperatura pero con algún tipo de oposición que constituye la resistencia térmica, por lo cual:

De tal manera que la conducción estable se puede solucionar a partir de un circuito térmico que puede presentar resistencias en serie y/o paralelo de acuerdo con el área compartida de transferencia de calor.
Ejemplo: Determine el calor transferido por las paredes A y B, y la temperatura de interfase Ti para la configuración geométrica y condiciones que aparecen en la figura 20.
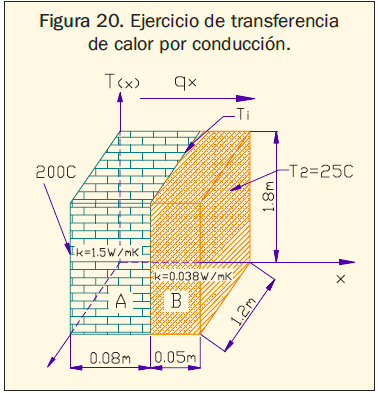
Solución: en la Tabla 4 se encuentra descrito el procedimiento para dar solución al ejercicio.


La ecuación de difusión de calor se puede transformar en coordenadas cilíndricas y esféricas para geometrías particulares con los siguientes resultados:
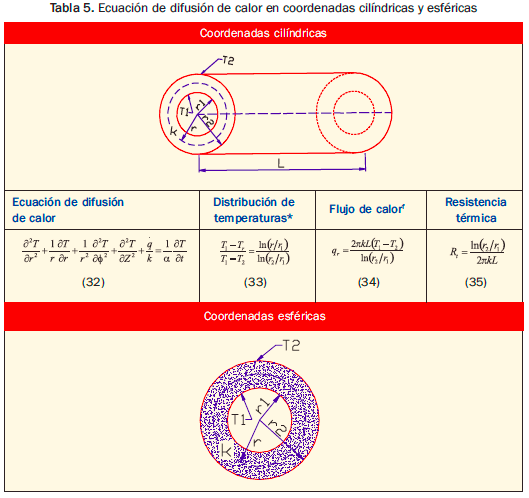

*Fuente: Jorge René Silva Larrotta, Introducción A La Termografía Industrial. Universidad Libre – Bogotá. 2006. ISBN 978-958-97987-0-6
