¿Cómo se puede aplicar la Termografía en la Industria? – Caldera Pirotubular.*

OBJETIVOS ESPECÍFICOS

1. Desarrollar una metodología para auditar equipos con pérdidas de energía térmica a través de la técnica de termografía.
2. Determinar las pérdidas de energía de la caldera pirotubular a través de la superficie en su estado actual y con la implementación de aislamiento térmico adicional.
3. Validar la modelación térmica de una caldera por elementos finitos a través de termografía.

EQUIPO MONITOREADO POR TERMOGRAFÍA

Caldera pirotubular horizontal de retorno.

• Capacidad: 5 BHP.
• Combustible: ACPM.
• Máxima presi.n admisible de trabajo: 100 psi.
• Presión de operación: 50 psi.
• Blindaje contra la radiación en acero inoxidable, exceptuando las tapas frontal y posterior.

PROCEDIMIENTO

1. Programación de la presión de operación (50 psi) y del tiempo de suministro de vapor para simular una operación normal de trabajo.
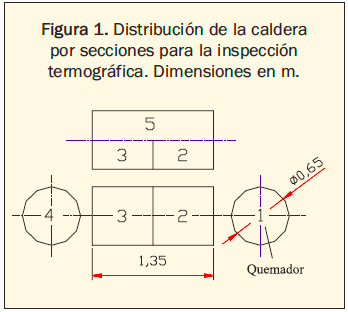
2. Definición de las 5 secciones de la caldera a monitorear, como se observa en la figura 1.
3. Reducción del efecto de las superficies especulares en las secciones 2,3 y 5 a partir de cubrimientos zonificados.
4. Calibración de la cámara termográfica (emisividad, rango de temperaturas, humedad relativa, temperatura ambiente y distancia foco – objeto).
5. Encendido de la caldera previa verificación del nivel de agua, suministro de combustible y sistema de control. (No se realizó ningún procedimiento de calibración en la combustión de la caldera.
6. Termografía por secciones entre intervalos de 10 minutos aproximadamente durante el encendido hasta llegar a la presión de operación.
7. Apertura de la válvula de suministro de vapor e inicio de nuevas tomas termográficas cada 10 minutos hasta terminar la reserva de vapor.
8. Apagado de la caldera y toma final de termografía.
9. Repetición del procedimiento en cinco ocasiones cada tercer día.
10. Instalación de aislamiento térmico adicional sobre las superficies (figura 2). Material donado por la empresa Fiber- Glass Colombia S.A de referencia Flex Wrap de 3 pulgadas de espesor previo cálculo manual y con el software Eco Win [3], a partir de los promedios de las temperaturas mas críticas para garantizar una temperatura de superficie inferior a los 30^oC y una eficiencia de aislamiento superior al 95%.
11. Repetición del paso 3 hasta el paso 9.
12. Preparación de los diez reportes termográficos obtenidos con las mediciones.
13. Análisis de la información a partir de una metodología establecida.
14. Modelación por elementos finitos de la transferencia de calor para la caldera con y sin aislamiento.
15. Consolidación de resultados y conclusiones.

ANÁLISIS DE LA INFORMACIÓN (METODOLOGÍA)

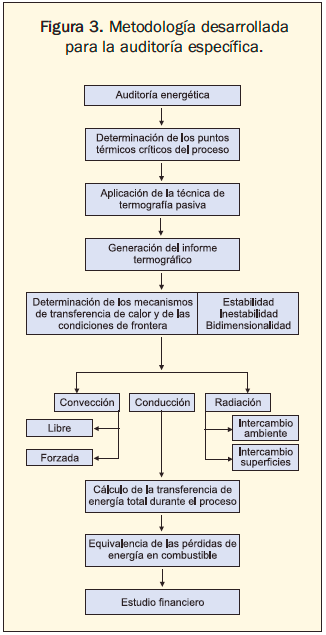
La metodología utilizada en el desarrollo de la investigación se encuentra en la figura 3, que puede considerarse como una alternativa para realizar auditorias específicas y detalladas en sistemas térmicos. A partir de la determinación de zonas críticas, previa auditoria energética general, se procede a realizar la termografía y a utilizar la teoría de los mecanismos de transferencia de calor combinados para establecer el equivalente de las pérdidas de energía en inversión.

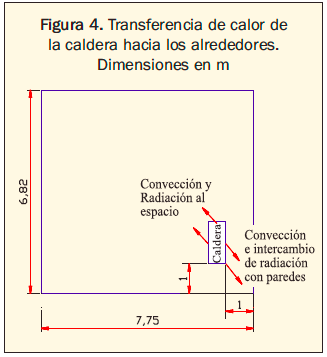
Para el caso estudiado la transferencia de energía térmica sucedió a través de los mecanismos de convección y radiación involucrados por la misma naturaleza del proceso y por la configuración y ubicación de la caldera, como se ilustra en la figura 4.

La metodología para calcular la transferencia de calor se explica a continuación:

TRANSFERENCIA DE CALOR

1. Convección

El coeficiente medio de transferencia de calor por convección se determinó por el método empírico para la determinación del número de Nusselt (Nu) a través de las correlaciones de parámetros adimensionales para un flujo externo sobre superficies con convección natural (Tabla 1), recomendada por Churchill y Chu¹ para paredes verticales y para cilindros horizontales de acuerdo con la secciÓn estudiada y con las propiedades del aire a la temperatura media entre temperatura ambiente y temperatura de superficie obtenida del reporte termográfico con el software ThermaCAM Reporter 2000®.

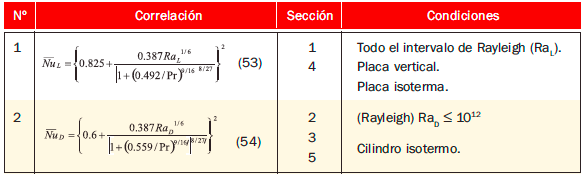
A partir del coeficiente de transferencia de calor por convección se determinó la transferencia de calor utilizando la ley de enfriamiento de Newton en cada sección de la caldera y en cada procedimiento de termografía, tanto para aislamiento térmico adicional como sin él, así como se observa en la tabla 2.

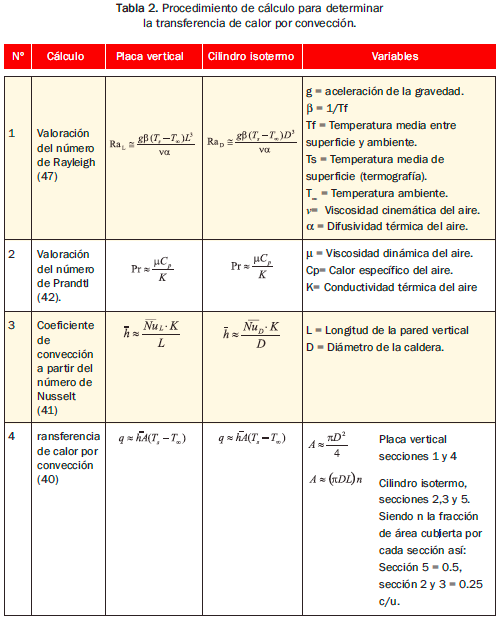
Es importante aclarar que las condiciones para determinar el número de Nusselt de la Tabla 1 no tienen una correspondencia directa con el caso particular en geometría y estabilidad, sin embargo los resultados presentan una aproximación válida teniendo en cuenta las siguientes consideraciones:

• La aplicación de la correlación 1 de placa vertical a las tapas circulares de la caldera se realiza asumiendo que el coeficiente de convección calculado en la superficie es independiente de su geometría dado que la sección circular puede estar contenida en una placa rectangular o cuadrada de lados equivalentes al diámetro de la tapa, de manera que la longitud característica de la placa se reemplaza por el diámetro en la determinación del número de Rayleigh.
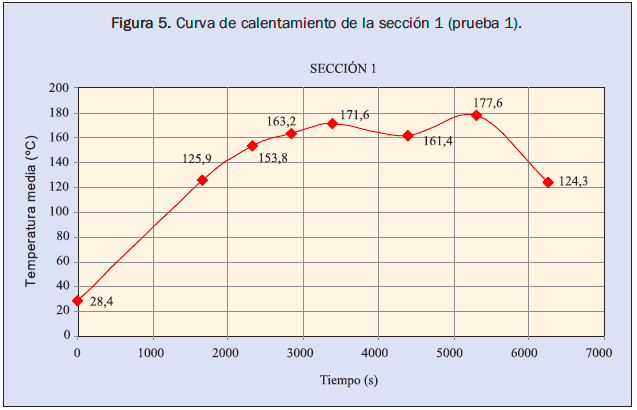
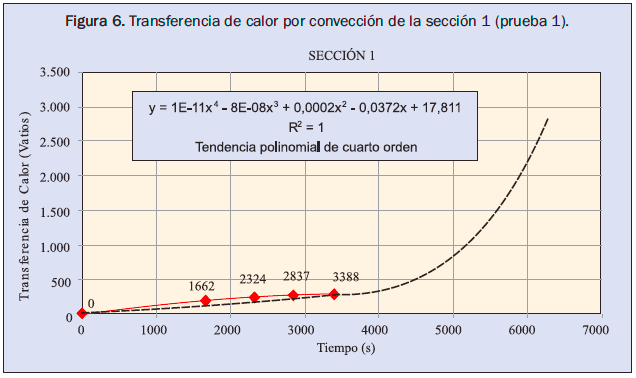
• Durante el calentamiento (encendido de la caldera hasta la presión de operación) las temperaturas de las superficies no son isotermas, por tal razón se realizaron mediciones en intervalos de tiempo muy cortos para considerar que el proceso está constituido por etapas cuasiestables, que al ser analizadas separadamente y posteriormente ensambladas determinan la curva de calentamiento de las secciones y la energía disipada durante este proceso. Las figuras 5 y 6 ilustran un ejemplo de la curva de calentamiento de la sección 1 y la transferencia de calor por convección de esa misma sección utilizando el procedimiento descrito anteriormente.
• La condición de sistema estable es válida después de que la caldera alcanza la presión de operación de 50 psi y las temperaturas se mantienen en márgenes estrechas de variación.

2. Radiación

Por la ubicación de la caldera y los materiales superficiales fue necesario calcular el intercambio de radiación térmica por separado entre secciones as.:

• Secciones 1 y 5: intercambio de radiación con las paredes del recinto.
• Secciones 2,3 y 4: radiación emitida al espacio.

En todos los casos las superficies fuero consideradas grises y difusas con propiedade radiativas hemisféricas totales.

El intercambio de calor entre las paredes del recinto se determinó a partir del circuito térmico que involucró dos resistencias de las superficies (caldera y pared) y la resistencia del espacio (figura 7).

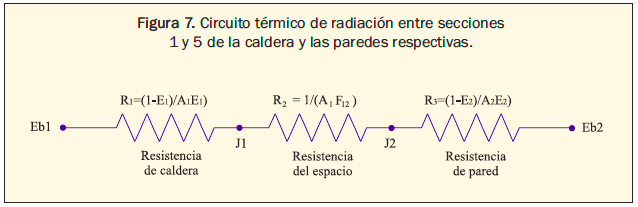
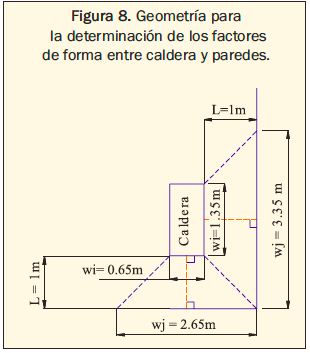
Los valores de emisividad en paredes y superficies de la caldera 1 y 4 se determinaron con la cámara a partir de la calibración utilizando el método de la cinta negra². Para las superficies en acero inoxidable la emisividad se estimó de acuerdo con las características del material en la guía de termografía³. Para la determinación de los factores de forma en las secciones 1 y 5 se utilizó la geometría de placas paralelas con líneas medias conectadas por una perpendicular⁴ como se observa en la figura 8.

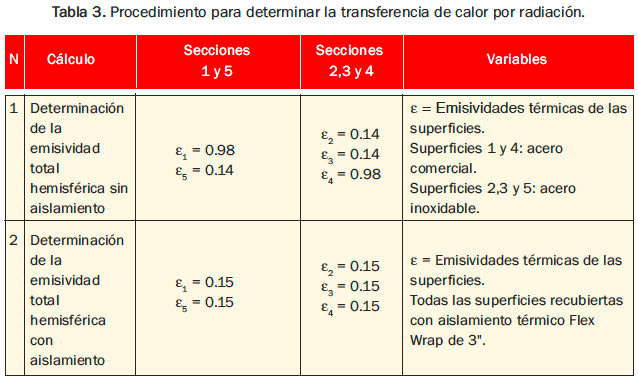
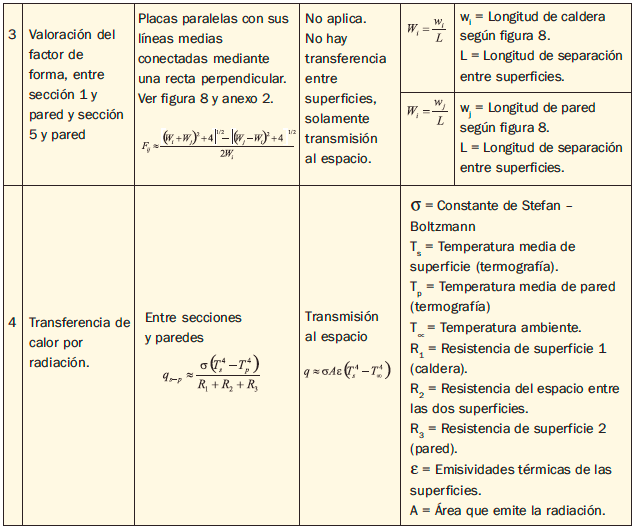
Con la información anterior se pudo determinar la transferencia de calor por radiación en las secciones de la caldera, por cada valoración de termografía y con la condición de aislamiento térmico adicional y sin el. En la tabla 3 aparecen las ecuaciones y variables involucradas.

RESULTADOS

La validez de los resultados corresponde al experimento bajo las condiciones descritas y es una primera aproximación a lo que podría ser la operación de una caldera de baja capacidad en algún proceso. Por las limitaciones del laboratorio y de las pruebas experimentales, no fue posible realizar la simulación concreta de un proceso específico, sin embargo el trabajo desarrollado permite establecer una metodología general de análisis térmico e ilustra al estudiante de ingeniería la relación directa entre la teoría de transferencia de calor y el mantenimiento.

Para cada inspección termográfica se realizaron los cálculos mencionados anteriormente determinando la transferencia de calor simultánea por convección y radiación por secciones, etapas de operación y tipos de aislamientos.

En las figuras 9 y 10 se presentan los consolidados de las pérdidas de calor en las secciones de la caldera durante los primeros experimentos de cada caso.

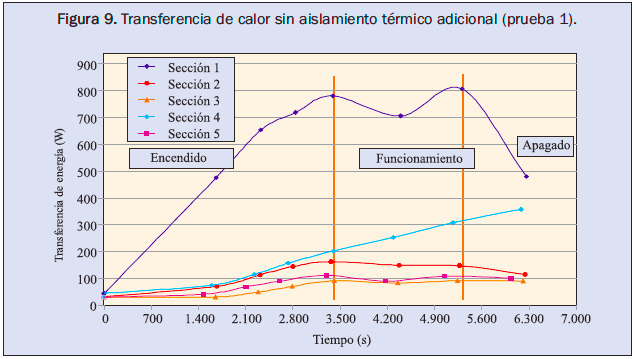
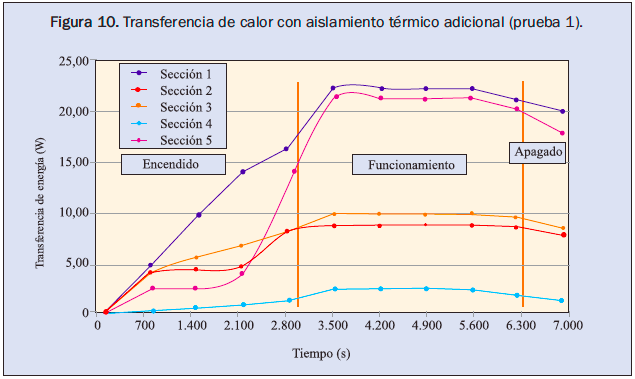
Se identifican las etapas experimentales de encendido, funcionamiento y terminación; y se observa que durante el funcionamiento se presentan oscilaciones entre intervalos relativamente pequeños, razón por la cual se hizo la consideración de estabilidad en dicha etapa. Es notoria la reducción en la transferencia de energía después de instalar el aislamiento.

1. Etapa de encendido

Durante el encendido se calculó la transferencia de energía y la energía total disipada a través de la integración de las curvas de calentamiento, ajustadas a polinomios de cuarto orden. Se destacan las secciones 1 y 4 como las de mayor pérdida de energía⁵ (figuras 11 y 12) sin embargo existe una notoria diferencia entre los resultados obtenidos con y sin aislamiento térmico, principalmente porque se redujo la temperatura promedio de superficie de 125 ^oC a 32 ^oC ocasionando un descenso en el gradiente de temperatura que determina la transferencia de calor por convección y una modificación en la emisividad promedio de las superficies a través del recubrimiento en aluminio que presenta el aislamiento, pasando de 0.98 a 0.15.

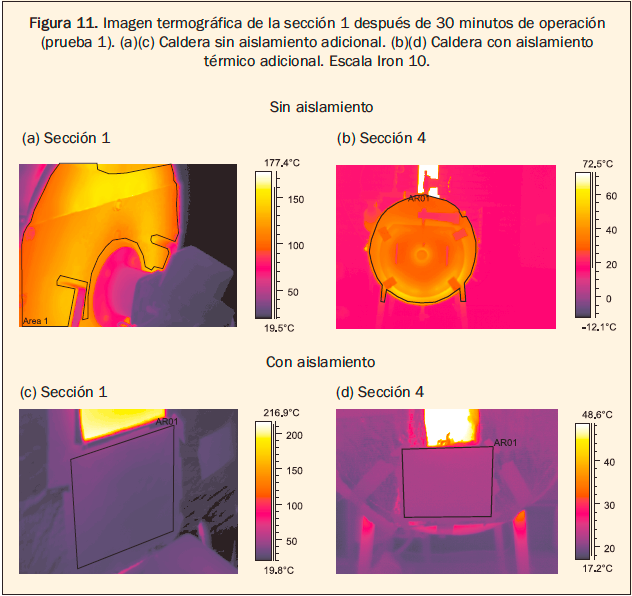
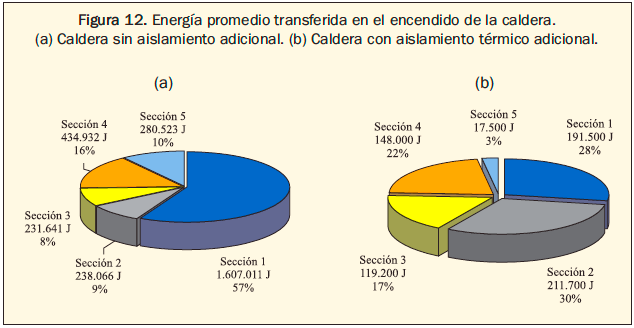
A pesar de las temperaturas bajas para considerar significativa la radiación, de acuerdo con algunos autores, resulta ser el mecanismo de transferencia más importante durante esta etapa.

El consolidado de la energía total transmitida discriminado por los mecanismos de transferencia de calor se representa en la figura 13.

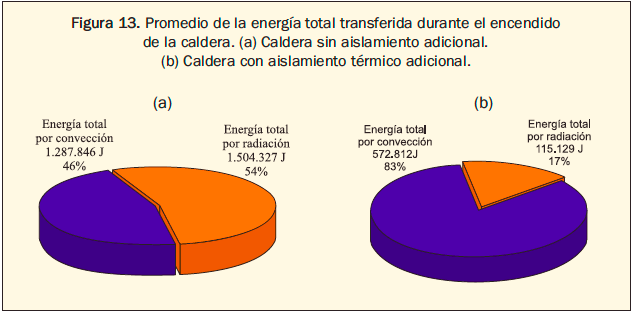
2. Etapa de operación

Se realizaron los mismos cálculos de la etapa de encendido, sin embargo no se consolidó la energía total transmitida por su dependencia al tiempo de operación y a las condiciones de vapor demandadas por el proceso particular que se pretenda simular.

Por la consideración de estabilidad relativa de las propiedades que intervienen en los mecanismos (emisividad, temperatura ambiente, temperatura de superficie, coeficiente de transferencia de calor por convección, etc), para efectos de cálculo, se promediaron los valores de transferencia de calor de las cuatro últimas tomas en cada prueba (figuras 9 y 10).

Los resultados reflejan que los dos mecanismos resultan importantes en magnitud y en participación. El aporte de la convección se incrementa en relación con la etapa de encendido debido al incremento en la diferencia de las temperaturas con relación al ambiente.

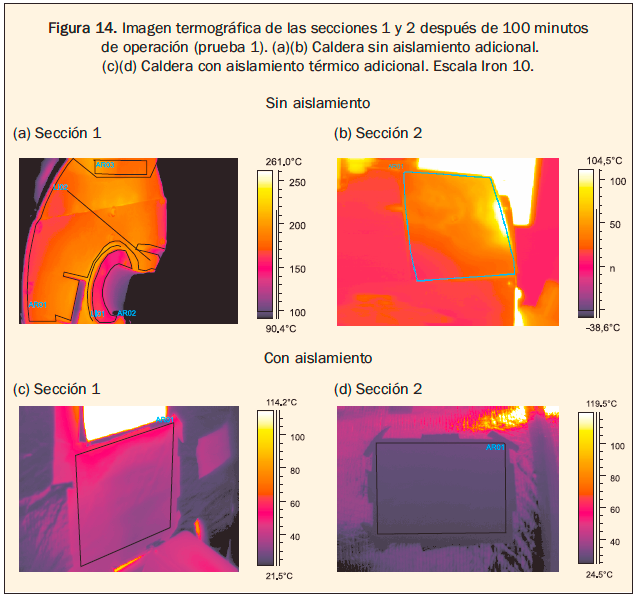
También se hace evidente la significativa reducción de la transferencia de energía cuando se implementa el aislamiento, como se presenta en la figura 14.

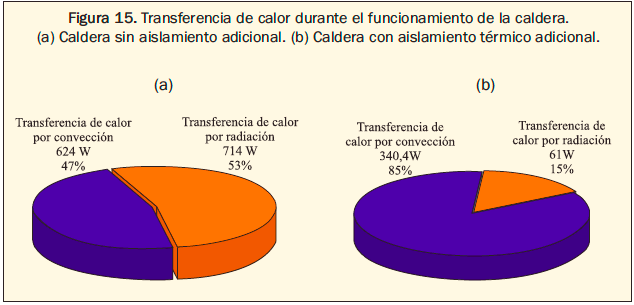
Los promedios de la transferencia de calor emitida por los mecanismos de transferencia de calor se encuentran en la figura 15.

3. Pérdidas equivalentes en combustible

Se determinaron bajo las siguientes condiciones:

• Las pérdidas equivalentes se calcularon con el poder calorífico superior del combustible (ACPM) de Colombia, 139660 Btu/gal⁶.
• En el cálculo no se involucró ningún parámetro de funcionamiento de la caldera.
• En el encendido las pérdidas se totalizaron durante los promedios del tiempo de duración.
• Durante la operación se estimaron por hora de funcionamiento para los casos experimentales que se trabajaron con la presunción de comportamiento estable.

En la tabla 4 se encuentran las pérdida equivalentes calculadas para los dos casos.

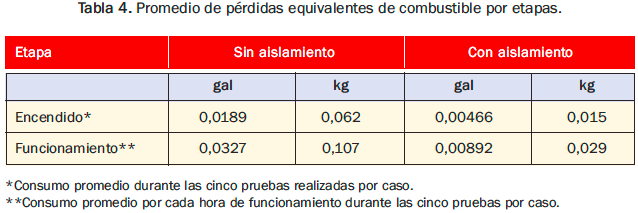
En un sistema de suministro de vapor en operación, las pérdidas por convección y radiación en la caldera estarían en función de las variables del proceso principalmente de la presión de operación, del tipo de combustible y de los ciclos de trabajo; lo que daría como resultado mayores pérdidas que las estimadas según la aplicación.

Los valores de la caldera sin aislamiento adicional representan entre el 5.3% y el 6.2% del combustible promedio total consumido (0,95 galones) durante el encendido y la extrapolación de una hora de funcionamiento. Porcentaje que resulta significativo para una caldera con una operación regular mensual, si se tiene en cuenta que es un equipo de pequeña capacidad (5 BHP) que presenta un bajo consumo de combustible.

Por el contrario, con el aislamiento térmico tales cifras se reducen a un porcentaje del 1.4% como resultado de la disminución de las pérdidas de energía en un 75% durante el encendido y en un 70% durante el funcionamiento.

4. Modelación por elementos finitos

Los resultados obtenidos anteriormente, llevaron a la formulación de un tercer estudio, que al momento se está iniciando, para evaluar las dos condiciones de aislamiento mediante la modelación de la caldera en un software CAD y otro CAE. Se ha utilizado un equipo con altas prestaciones de servicio con las siguientes características:

• Procesador Athlon de 3 Ghz.
• 1 Giga de memoria RAM.
• Disco duro de 80 Gigas.
• 128 Mb de memoria en video.

Las principales etapas en que se ha desarrollado el proyecto se resumen así:

1. Levantamiento de los planos de la caldera.
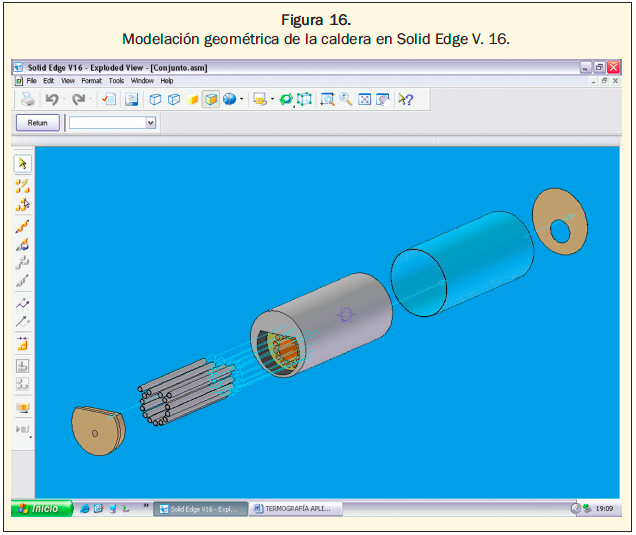
2. Construcción geométrica del modelo en 3D a través de un software CAD especializado: “Solid Edge V.16” (figura 16).

3. Importación de la geometría al software CAE especializado: “ANSYS Workbench V.10®” con el módulo de trabajo de carga térmica. El software reconoce la geometría como la formación de piezas independientes (figura 17), de tal forma que se pueden modificar al igual que sus parámetros.

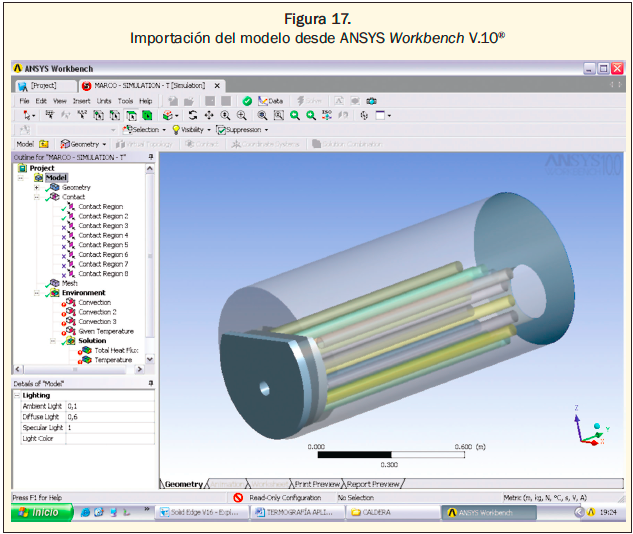
4. Definición de las características constructivas del modelo correspondientes a las propiedades de los materiales y a las zonas de contacto existentes entre las piezas que componen el conjunto.

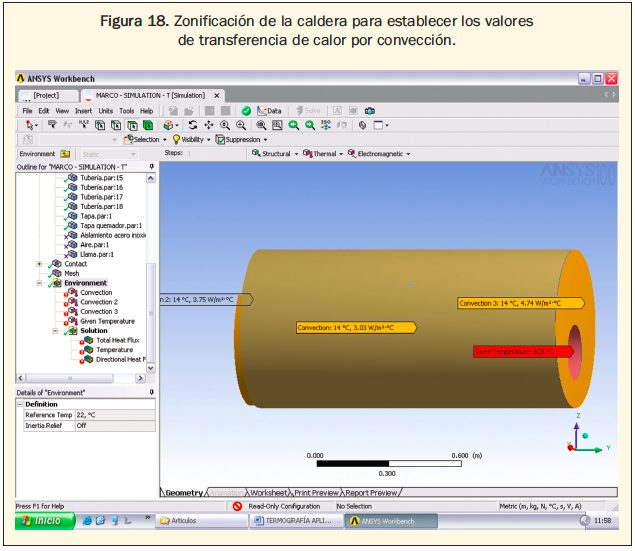
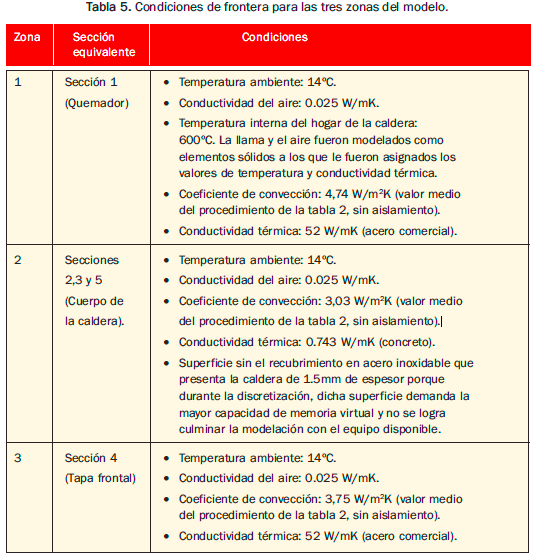
5. Definición de las condiciones de frontera del modelo, tales como coeficientes de convección y radiación, generación interna de calor, temperaturas superficiales iniciales, temperatura ambiente, etc. Para el proyecto se establecieron 3 zonas de transferencia de calor (figura 18) en concordancia con las zonas descritas en termografía, con las propiedades de la tabla 5.

Se realizaron tres modelaciones así:

• Primera modelación: la llama de combustión se definió como un elemento sólido cónico con una temperatura promedio de 1000 ^o C.
• Segunda modelación: se estableció el cono como unidad generadora interna de calor con un valor de 5,9774 E6 W/m³, en función del consumo y tipo de combustible.
• Tercera modelación: se trabajó dando una temperatura de 600 ^oC a la pared envolvente del hogar de la caldera.

Finalmente se consideró esta última como la primera aproximación dado que fue la que presentó resultados consistentes con las pruebas realizadas por termografía.

6. Discretización automática del modelo a través de configuraciones triangulares y rectangulares (figura 19).

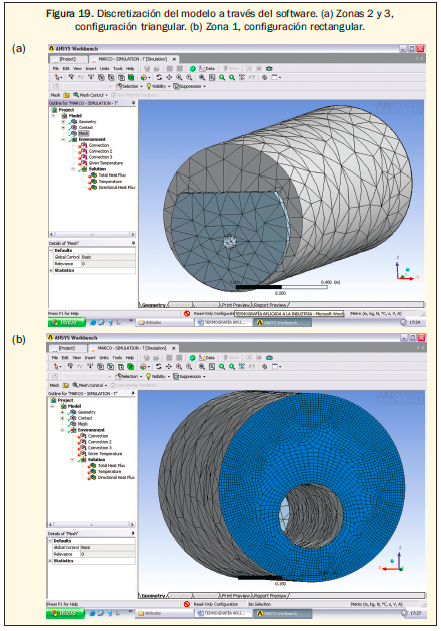
7. Solución automática de la distribución de temperaturas. ANSYS Workbench comienza a cargar todas las piezas, teniendo en cuenta los materiales y las zonas de contacto definidas previamente. Al cargar toda esta información se lleva a cabo la implementación del modelo matemático más aproximado para la carga, geometría y entorno establecido. El programa tardó aproximadamente 8 horas (figura 20).

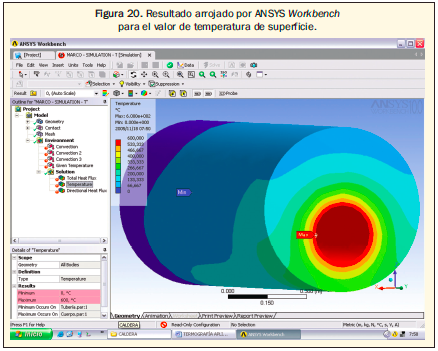
Los resultados presentan cierta congruencia entre la modelación y las condiciones establecidas inicialmente. En la tabla 6 se relacionan los valores de temperatura entre el termograma y la modelación térmica.

Aunque los valores de las secciones 2,3,4 y 5 no se aproximen a los determinados por la técnica de termografía, e incluso presenten desviaciones superiores al 50%, cuando se realizan los cálculos para determinar las pérdidas de calor por convección y radiación en la etapa de funcionamiento, con el mismo procedimiento de la auditoria por termografía, se encuentran valores muy cercanos, como se ilustra en las figura 21.

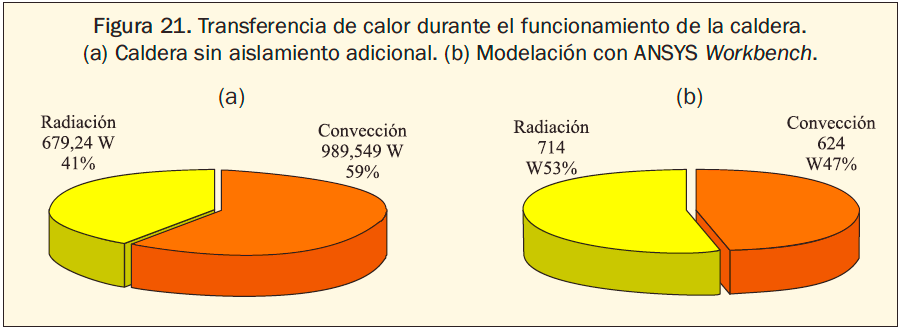
La diferencia entre las pérdidas totales de calor es menor al 20%, que para la aplicación particular, representa un error aceptable y un factor de seguridad para la selección del aislamiento térmico, dado que las mayores pérdidas se encuentran en la modelación con un valor de 1668.8 vatios, frente a 1338 vatios medidos a partir de las imágenes termográficas.

También es notorio el cambio en la participación de la radiación en la disipación de calor, pasando de un 53% a un 41% como resultado de la disminución de temperatura en las secciones 1 y 4, que no puede relacionarse de ninguna manera con la eliminación del recubrimiento del acero inoxidable como barrera de la radiación porque a pesar de no tenerse en cuenta en la modelación, en los cálculos de transferencia de calor por radiación sí, al considerar la emisividad de la superficie de 0.14 correspondiente a dicho material. Cuando se elimina el recubrimiento solamente se omite una superficie adicional de transferencia de calor por conducción cuya resistencia resulta despreciable por su bajo espesor (<1.5mm) y alta conductividad térmica (≈ 15W/mK) (3), con un valor cercano a 0.000058 K/W.

Los resultados llegan a ser entonces una primera aproximación para la determinación de la distribución de temperaturas en la caldera de estudio, sin embargo su validez presenta las limitaciones de la modelación que están asociadas a errores causados por las simplificaciones realizadas, sujetas a su vez a limitaciones en el recurso computacional.

CONCLUSIONES

1. La metodología empleada en el análisis de la información es válida en una auditoria energética específica y detallada de un equipo que transmita energía térmica no recuperable. Lo más importante es definir las condiciones de frontera del sistema a estudiar para aplicar un modelo teórico aproximado sobre unos resultados experimentales.
2. El informe termográfico no se puede limitar a la observación superficial de temperaturas para encontrar zonas con problemas, es necesario de acuerdo con la aplicación, un análisis profundo que determine su significado y las soluciones adecuadas.
3. La aplicación de la teoría de transferencia de calor al mantenimiento industrial favorece ampliamente la implementación de programas de administración de energía, la comprensión de los fenómenos térmicos e ilustra al estudiante de pregrado sobre el uso práctico de la academia.
4. A través del monitoreo realizado a la caldera se pueden establecer las pérdidas de calor por secciones y por etapas de operación, de manera que se determinen las zonas críticas de aislamiento y la recuperación de la inversión por la implementación de nuevo material. En el caso particular, con el supuesto de una jornada de trabajo para el equipo de 8 horas diarias, la recuperación de la inversión se verifica a los 8 meses de la instalación, aproximadamente.
5. Con los nuevos desarrollos en los paquetes de elementos finitos y hardware, fácilmente podrá evaluarse el comportamiento térmico de cualquier sistema por complejo que sea y sus respuestas a modificaciones en las variables del proceso, con una adecuada validación a través de la técnica de termografía.

1. INCROPERA y DeWITT. Fundamentos de Transferencia de Calor. México. Prentice Hall, 1999, cap. 9,
   pp. 492 – 504. ↩︎
2. El método consiste en colocar una cinta negra con emisividad conocida (generalmente 0.98) sobre la superficie que se desea medir; posteriormente con la cámara termográfica se mide su temperatura, luego se retira y se vuelve a realizar la medición en el sitio donde se encontraba la cinta cambiando la emisividad en la cámara hasta llegar a la temperatura anterior. Cuando se alcanza dicho valor se ha encontrado la emisividad del material sobre el cual fue puesta la cinta. ↩︎
3. ThermaCAM. Operator‘s Manual. USA. Flir Systems. 2000. cap 11. ↩︎
4. CENGEL YUNUS A. Transferencia de calor. México: Mc Graw Hill, 2004, cap 12. pp. 609 – 610. ↩︎
5. La sección 1 corresponde a la superficie donde se aloja el quemador y por tanto la de mayores temperaturas. ↩︎
6. ECOPETROL. Empresa Colombiana de Petróleo. Departamento de Ingeniería de Proceso. ↩︎

*Fuente: Jorge René Silva Larrotta, Introducción A La Termografía Industrial. Universidad Libre – Bogotá. 2006. ISBN 978-958-97987-0-6